An assessment of the simple majority rule
- baptistedefontenay
- Jul 11, 2024
- 10 min read
Introduction
Many fundamental decisions in democracies are made by aggregating citizens’ individual preferences or opinions, usually collected through a vote, into a societal choice. Picking the most appropriate aggregating rule for each circumstance is a topical issue. In France, president Macron promised to boost proportional representation in legislative elections, while, in the US, former president Trump called “crazy” the Senate supermajority rule. Generally, the simple majority rule has been the prominent social choice rule in democracies, including in referendums, jury verdicts, and legislation. This prompts the question: Is the simple majority rule suitable for all types of decisions?
This essay will first evaluate the case for simple majority rule when deciding between two alternatives. Second, how the simple majority rule performs under more than two alternatives. Then, we will investigate how the probability of cycles can be reduced by imposing supermajority rules. Finally, we will examine whether the asymmetric treatment of alternatives under supermajority rules, in contrast to the inherent neutrality under simple majority, is ever justified.

Aggregating over two alternatives
When aggregating individual votes over two alternatives, the simple majority rule selects the option with the majority of votes. Three strong normative arguments support the use of the simple majority rule in decisions between two alternatives.
First, when aggregating preferences over two alternatives, such as in referendums and legislature votes, May’s theorem states that the simple majority rule is the only choice function satisfying four desirable procedural requirements characterising the relationship between individual inputs and social decisions (May, 1952). These four requirements are decisiveness, which ensures that the social choice function makes a unique choice for any set of individual preferences; anonymity, which requires that all individuals are treated the same; neutrality, which requires that all alternatives are treated the same; and positive responsiveness, which requires the output to be a positive function of the individual inputs. If we believe these axioms are necessary, which is often the case as they encapsulate the basic principles of democracy[1], we have a strong procedural case for the simple majority rule.
Furthermore, when aggregating preferences, the Rae-Taylor theorem states that the simple majority rule is the only rule that maximises each decision-maker’s expected utility (Mueller, 2003). This only holds under two strong assumptions: all individuals have an equal prior probability of preferring each alternative and face equal intensities on each issue[2]. More generally, the simple majority rule minimises the number of frustrated voters (Brighouse and Fleurbaey, 2010) – a strong utilitarian argument for using the simple majority rule.
Lastly, when the aim of the social decision is to aggregate information to make a judgement over two states of the world, such as in a jury’s verdict, the Condorcet Jury Theorem (1785) states that the decision made using the simple majority will tend to the truth with probability approaching one as the number of voters increases[3]. Hence, Ben-Yashar and Nitzan (1997) proved that if committee members are equally skilled, a committee should use the simple majority rule to decide whether to pursue a project. Whether the competence[4] and independence assumptions used in the theorem hold in practice is specific to each decision and requires empirical study.
Aggregating over more than two alternatives
When aggregating votes over more than two alternatives, the simple majority rule chooses as the new status quo any proposal, which any agent can make, that commands a simple majority against the existing status quo.
When aggregating individual preferences over more than two alternatives, the simple majority rule can yield intransitive social preferences. For example, suppose there are three alternatives, x, y, and z, and three voters. If voter one prefers x to y to z, voter two prefers y to z to x, and voter three prefers z to x to y. Each alternative is beaten by another alternative in a pairwise vote by majority: x is preferred to y, z is preferred to x, and y is preferred to z. This is called the Condorcet paradox. In Arrow’s axiom framework, the simple majority rule fails the transitivity property, i.e., if society prefers x to y and y to z, then society cannot prefer z to x. More generally, Arrow’s theorem states that under more than two alternatives, no aggregation rule simultaneously satisfies five axioms: independence of irrelevant alternatives, non-dictatorship, Pareto criterion, unrestricted domains, and transitivity (Arrow, 1951).
Nevertheless, the simple majority rule is not always intransitive under more than two alternatives. If we impose two restrictions: the issue on which individuals vote has one dimension and individuals have single-peaked preferences[5] over the alternatives, then there exists a unique simple majority winner (Median Voter Theorem, Black, 1948). The social choice follows the median voter's preferences, whose most preferred outcome is Condorcet Winner, i.e., an alternative that commands a simple majority against any other feasible alternative in a pairwise comparison. The simple majority rule then satisfies the rest of Arrow's axioms. Other domain restrictions that yield similar properties include separability into two groups (Inada, 1964), single-cavedness (ibid), and latin squarelessness (Ward, 1965).
Under which circumstances such preferences appear in the real world is a continuing debate. On some legislative issues, such as tax and quantity of public goods, voters likely have a unique preferred level and rank all levels adversely as they get further from their ideal point (see Figure 1). Practically, Poole and Rosenthal (1985) successfully classified 81 percent of the votes in the U.S. Senate with a single dimension (the underlying "ideological" dimension). Furthermore, Miller (1992) proved that group deliberation can induce single-peaked preferences. In elections, Caplin and Nalebuff (1991) argue that the Median Voter theorem does not apply as candidates vary in other dimensions than their position on the political spectrum. Indeed, except for strongly polarising candidates, such as Jean-Marie Le Pen in the 2002 French presidential election, who created “transitivity-allowing” preferences (Dasgupta and Maskin, 2008), Clarke et al., (2011) found that other factors, such as leader “images,” can impact voters’ decisions.
For an issue that can reasonably be considered unidimensional and single-peaked (such as the government size), Aidt and Jensen (2013) empirically confirmed the Median Voter theorem by finding a positive relationship between the franchise and government spending per capita in Western Europe between 1820 and 1913.
Simple majority rule over multi-dimensional issues
Under multidimensional issues, even if preferences over each issue are single-peaked, the Median Voter theorem fails, and the simple majority rule yields intransitive social preferences. Plott (1967) proved that a majority rule equilibrium exists under majority voting over multidimensional issues. Still, his restrictions are so demanding that they appear inapplicable to economic questions. This is a serious problem as, given the nonexistence of a Condorcet winner, it is always possible to design a series of majority victories leading from any starting point to any outcome (The Chaos Theorem), yielding a lot of power to the agenda setter and creating incentives to misrepresent preferences.
Supermajority rules as a solution to reduce the probability of cycles
The probability of cycles can be reduced by imposing a supermajority rule – i.e., increasing the required majority to defeat the status quo. Greenberg (1979) proved that the level of majority needed m* must satisfy:
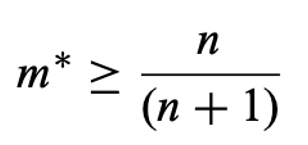
to guarantee that at least one equilibrium point exists. This assumes that individuals have convex preferences over an n-dimensional space. In 1988, Caplin and Nalebuff proved that the minimum m* diminishes to:
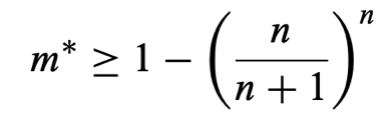
, assuming a generalised single peakedness in more than one direction and a degree of social consensus, which can be credible assumptions. As n tends to infinity, this condition implies that a 64% majority will be sufficient to ensure at least one equilibrium point exists for an n-dimensional space.
On the neutrality of social rules
What differentiates supermajority rules from the simple majority rule is neutrality. Under the simple majority rule, all alternatives are treated equally, while under supermajority, the status quo is privileged.
When aggregating information, imposing neutrality over alternatives via the simple majority rule maximises the probability that the truth coincides with the collective decision yielded by our social choice function. Yet, in certain circumstances, favouring one alternative, despite reducing the chance of accurately identifying the true state, is justified. This occurs when choosing a particular alternative incurs significant costs, as in a guilty verdict in a jury’s decision. Voltaire’s sentiment, "it is better to risk sparing a guilty man than to condemn an innocent one" (Voltaire, 1748, as translated in Pearson, 2006, p 124), supports this. Hence, in circumstances involving a socially costly alternative, such as in a jury’s verdict, supermajority rules are preferred to reduce the probability of wrongly choosing the costly alternative.
When aggregating preferences, neutrality among alternatives is key to embodying the values of political equality (Dahl, 1956). Hence, in most circumstances, such as elections, a simple majority is more suitable than supermajority rules to maintain political equality. In specific circumstances, we might also be concerned with protecting minorities. Some have argued that the simple majority rule leads to the "tyranny of the majority" (Mill, 1859), as "the few are at the mercy of the many" (Adams, 1851, p 134). Bradbury and Johnson (2006) found evidence that supermajority rules can reduce the "tyranny of majority spending" when analysing US states redistributive spending between 1960 and 1997. More generally, it is evident that, at least through veto, supermajority rules empower minorities to prevent changes to the status quo they do not favour (Guinier, 1994). The notion that supermajority rules always better protect minorities than the simple majority rule has been criticized. For example, McGann (2002) argues that simple majority rule offers more protection to all minorities as minorities can more easily form a coalition to change the status quo. In general, minorities benefit from supermajority rules only when they are more at threat from a change in the status quo than from a failure to change the status quo, as seen in constitutional rights votes. This establishes a trade-off between political equality (best served by the simple majority rule) and protection of minorities (best served by supermajority rules), which must be evaluated in each situation. For example, in constitutional votes, which can threaten minorities fundamental rights, prioritising minority protection over political equality is justified, so a supermajority rule is preferable.
Conclusion
Given the widespread use of the simple majority rule, I find it encouraging that it enjoys a robust normative support. Nevertheless, the simple majority often yields intransitive social preferences when aggregating votes over multi-dimensional alternatives, leading to chaotic decisions. In those circumstances, supermajority rules can sometimes ensure a majority equilibrium exists. The assumption of neutrality inherent in the simple majority rule is almost always desirable. Using supermajority rules is only suitable when one alternative is costly and when we want to prioritise minority protection.
Several points limit our conclusions. First, we have restricted our attention to social decisions with a single winner and bypassed the question of who should vote. We also implicitly ruled out interpersonal comparisons, while additional information to ordinal preferences, such as interpersonally comparable welfare may be justifiable (Sen 1982).
[1] Neutrality is discussed in the last part
[2] i.e., the gain experienced from a favourable outcome equals the loss from an unfavourable outcome
[3] Assuming independence and competence
[4] i.e., probability of being right > 1/2
[5] i.e., alternatives can be positioned on a line and individuals have a globally most-preferred position with decreasing preference as alternatives get further away from the most preferred position.
This essay was written for a microeconomics home assignment in my master's at Cambridge.
Evaluate the case for adopting the simple majority rule to make collective decisions in a diverse set of circumstances. Is there ever a case for adopting a stricter rule such as a two-thirds majority rule?
Annex
Figure 1: Single-peaked preferences over a public good (figure from Mueller, 2003)

The median voter, m, decides under simple majority rule.
Bibliography
Adams, J. (1851) The Works of John Adams, Second President of the United States With a Life of the Author, Notes and Illustrations, Vol. 6, Little, Brown and Company
Aidt, T. S. and Jensen, P. S. (2013) ‘Democratization and the Size of Government: Evidence from the Long 19th Century.’, Public Choice, Vol. 157, pp. 511–42.
Arrow, K. J. (1951) Social choice and individual values. 1st edn. Wiley, New York
Ben-Yashar, R. C. and Nitzan, S. I. (1997) ‘The Optimal Decision Rule for Fixed-Size Committees in Dichotomous Choice Situations: The General Result’, International Economic Review, Vol. 38, No. 1, pp. 175-186 doi: 10.2307/2527413
Black, D. (1948) ‘On the Rationale of Group Decision-making’, Journal of Political Economy, Vol. 56, No. 1, pp. 23-34
Bradbury, J. C. and Johnson, M. J. (2006) ‘Do Supermajority Rules Limit or Enhance Majority Tyranny? Evidence from the US States, 1960-1997’, Public Choice, Vol. 127, No. 3/4, pp. 437-449
Brighouse, H. and Fleurbaey, M. (2010) ‘Democracy and Proportionality’, Journal of Political Philosophy, 18 (2), pp. 137–155 doi: 10.1111/j.1467-9760.2008.00316
Caplin, A. and Nalebuff, B. (1988) ‘On 64%-Majority Rule’, Econometrica, Vol. 56, No. 4, pp. 787-814 doi: 10.2307/1912699
Caplin, A. and Nalebuff, B. (1991) ‘Aggregation and Social Choice: A Mean Voter Theorem’, Econometrica, Vol. 59, No.1, pp. 1-23 doi: 10.2307/2938238
Clarke, H., Sanders, D., Stewart, M. C., and Whiteley, P. (2011) ‘Valence politics and electoral choice in Britain, 2010’, Journal of Elections, Public Opinion and Parties, 21(2), pp. 237–253
Condorcet, N.C. (1785) Essai sur l’application de l’analyse à la probabilité des decisions rendues à la pluralité des voix. Imprimerie Royale, Paris
Dahl, R. (1956) A Preface to Democratic Theory. University of Chicago Press
Dasgupta, P. and Maskin, E. (2008) ‘On the Robustness of Majority Rule’, Journal of the European Economic Association, Vol. 6, pp. 949–973
Gerhardt, M. J. (1991) ‘The Role of Precedent in Constitutional Decision-making and Theory’, Faculty Publications
Greenberg, J. (1979) ‘Consistent Majority Rules over Compact Sets of Alternatives’, Econometrica, Vol. 47, No. 3, pp. 627-636
Guinier, L. (1994) The Tyranny of the Majority: Fundamental Fairness in Representative Democracy. Free Press
Inada, K. (1964) ‘A Note on the Simple Majority Decision Rule’, Econometrica, Vol. 32, No. 4, pp. 525-531 doi: 10.2307/191017
Marshall, B. (1994) ‘A Review of Lani Guinier's "The Tyranny of the Majority"’, Yale Law & Policy Review, Vol. 12, No. 2, pp. 541-547
May, K. O. (1952) ‘A set of independent necessary and sufficient conditions for simple majority decision’, Econometrica, Vol. 20, No. 4, pp. 680–684
McGann, A. J. (2002) ‘The Tyranny of the Super-Majority: How Majority Rule Protects Minorities’, UC Irvine: Center for the Study of Democracy
Mill, J. S. (1859) On Liberty. Broadview Press
Miller, D. (1992) ‘Deliberative Democracy and Social Choice’, Political Studies, Vol. 1, pp. 54-67
Mueller, D. C. (2003) Public Choice III. Cambridge University Press
Pearson, R. (2006) Voltaire Candide and other stories. Oxford World’s Classic, pp. 110-181
Plott, C. R. (1967) ‘A Notion of Equilibrium and its Possibility Under Majority Rule’, The American Economic Review, Vol. 57, No. 4, pp. 787-806
Poole, K. T. and Rosenthal, H. (1985) ‘A Spatial Model for Legislative Roll Call Analysis’, American Journal of Political Science, Vol. 29, No. 2, pp. 357-384 doi: 10.2307/2111172
Sen, A. (1982) Choice, Welfare and Measurement. Oxford: Basil Blackwell
Ward, B. (1965) ‘Majority Voting and Alternative Forms of Public Enterprises’ in Margolis, J. (ed.) The Public Economy of Urban Communities. Baltimore: Johns Hopkins Press, pp. 112-126 doi: 10.4324/9781315670805



Comments